[At]

Bobeau...  Bobboau... I was never really sure how to spell your name.  So, you're Bob-oh, now :P

Second and sadly, no I don't have a calculator.  That would require me to load a model and do intersection tests.  Atleast for the approximation I thought of.  Bob-oh prolly could give you a solution that's more exact with his funky Mathematica thing.


The Moment of Inertia Tensor

So.  Moment of Inertia.  No body but Bob-oh seemed sure what it was, and even he stated he didn't know how FS2's implementation worked.

I googled for "Inertia Matrix" and found physics lessons on how to calculate it.  It's also called, as Bob-oh said, an Inertia Tensor.

The Inertia matrix is a 3x3 thing (Yeah, we all know that!) with a bunch of floating point numbers.  A bunch of very small floating point numbers.  A bunch of very small floating point numbers that are smaller for larger ships.  Which doesn't make sense if we look at how to calculate even a simple MoI, let alone this tensor thing.

Time to start code browsing.

Allow me to present line 210 of physics.h :

Code: [Select]

matrix  I_body_inv;  // inverse moment of inertia tensor (used to calculate rotational effects)
It's the inverse!  This explains why the numbers are so small.  Conceptually, a matrix's inverse simple.  Let's say we have a 1x1 matrix A with 3 in that one cell.  If B is A's inverse, notationally B = A^-1, then A * B = I, where I is a 1x1 identity matrix, which in its single cell is the value 1.  This is like scalar multiplication.  If a * b = 1, then b must equal 1/a, or a^-1.

Calculating a bigger matrix's inverse, though, is a little more difficult given how matrix multiplication works.  Thankfully, there are places like Wikipedia that already have this worked out algebraically.

Why is it inversed, though?  Wouldn't it be easier just to store the regular moment of inertia?

If one were finding torque from an acceleration, this would be true.  In FS2, though, there's only one place where the Inertia tensor (matrix!) is used, and that's in the function physics_apply_whack() : (line 1139 of physics.cpp)

Code: [Select]

vm_vec_rotate( &delta_rotvel, &local_torque, &pi->I_body_inv );
First, they use the rotate function because rotating a vector through a matrix is done the same way as getting a torque from an acceleration vector and an inertia matrix.  Or, in this case, vice versa.

The syntax for vm_vec_rotate() is

Code: [Select]

vec3d *vm_vec_rotate( vec3d *dest, vec3d *src, matrix *m )
For two vectors dest and src, and one matrix m, dest = m * src;  See Note one at the bottom for this expanded.

Looking back at the line in physics_apply_whack(), we see that the destination is delta_rotvel, that the source vector is torque, and that the matrix involved is pi->I_body_inv, or the Inverse of the body's inertia tensor.

In standard physics, we know that Torque = MomentOfInertia * AngularAcceleration.  But here, we see that the physics is calculating the angular acceleration (well, FS2 physics are a litte different.  Dare I say... Whacked?) from an applied torque and the Inertia tensor.  Or inversed inertia tensor, in this case.

Torque = MomentOfInertia * AngularAcceleration;

So, AngularAcceleration = MomentOfInertia^-1 * Torque

Since this is the only place in the code that uses the Inertia tensor, it makes sense to store it inversed, as there are less calculations involved.


Calculating the Tensor

So, now we know why the Moment of Inertia numbers are the way they are.  How do we calculate them?

Integration is right out.  When was the last time you heard a GTF Hercules function?  This leaves summations.

Looking at any of the sites found on Google, we see that for

Code: [Select]

| I[x,x] I[x,y] I[x,z] |
| I[y,x] I[y,y] I[y,z] |
| I[z,x] I[z,y] I[z,z] |
I[x,x] = SUM m * ( x² + y² )
I[y,y] = SUM m * ( x² + y² )
I[z,z] = SUM m * ( x² + y² )

I[x,y] = I[y,x] = SUM m * x * y
I[x,z] = I[z,x] = SUM m * x * z
I[z,y] = I[y,z] = SUM m * y * z

(Note that this is why Bob-oh said there are only six values for the Inertia tensor rather than nine.)

Now, Bob-oh had some kind of funky Mathematica thing that calculates MoIs using a model's triangles.  That'd prolly be better to do, in the end, though anyone who doesn't understand what Bob-oh did won't have a chance to start just by staring at that omghax he made.

For an easier to understand approximation, which Bob-oh also alluded to, lets start with a shape and a grid.  And a density, if we want to assume a uniform density for the object in question.  (All the freespace ships have a density near water, if I recall what I heard correctly ;)

Calculating I[z,z] (SUM m * ( x² + y² )) and I[x,y] (SUM m * x * y), we make an array of boxes to approximate the shape along the Z axis, then sum the boxes' mass based on their volume (since mass = density * volume)



For a dodecahedron and an 8 by 8 grid, we get this extremely rough approximation by drawing boxes that meet the hedron at their centers.  (Like opproximating an integral using the midpoint rule.)




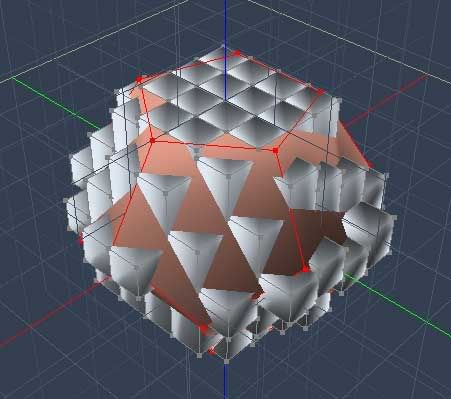
Since we know the X-Y coordinates of these boxes, we can just iterate over them, multiplying density by the volume for the mass, using their X-Y coordinates in the summation formulae.

The best part is that this also gives us an approximate volume.

This is repeated again for the X and Y axes.  The volumes could optionally be averaged together.


So!  Now that I've bored you all out of your brains, any questions?  Comments?  Corrections?

And no, again, I don't have an inertia tensor calculator.  But now, Bob-oh should be able to finish his, now that he knows how FS2 treats Inertia tensors.  Isn't that right, Bob-oh? ;)

And as a tangental thought, I wonder how hard it would be to change FS2 to rotate ships around their centers of mass...  Either that, or change all the POFs so that the ship's model centers to their CoMs?  Which would actually make for less data, even if not significantly...  Though it would eliminate The Baseball Manuever as a viable defense tactic.


Notes...

For two vectors dest and src, and one matrix m, dest = m * src

Expanded, this looks something like

Code: [Select]

| dest[x] |   | m[x,x] m[x,y] m[x,z] |   | src[x] |
| dest[y] | = | m[y,x] m[y,y] m[y,z] | x | src[y] |
| dest[z] |   | m[z,x] m[z,y] m[z,z] |   | src[z] |
Calculated,

Code: [Select]

| dest[x] |   | m[x,x] * src[x] + m[x,y] * src[y] + m[x,z] * src[z] |
| dest[y] | = | m[y,x] * src[x] + m[y,y] * src[y] + m[y,z] * src[z] |
| dest[z] |   | m[z,x] * src[x] + m[z,y] * src[y] + m[z,z] * src[z] |

[Herra Tohtori]

In short words: Will it be able to make a Newtonian flight model a possibility that could be chosen on if wanted in, say, BSG or B5 mod? :drools: Or is this just about turning issues (angular momentum and it's conservation)?

Or is this just a hobby? 

By the way, what you did by changing the dodecadron into cubes was effectively a low-resolution graphical integration. In true integration the only difference is that the cubes are reduced to infinitely small and added together...

I can image how it would be possible to make a logarithm (EDIT: LOL, this is one of the few places where it shows that I'm not a native English speaker, I did indeed mean algorithm  ) that counts an angular momentum of an object (proposed it had a static mass). Just divide it onto small enough parts (the smaller the pieces the better the accuracy) that have a center of mass known; then you can calculate the angular momentum of each of these centers of gravity around the main CG of the body. It all just adds up then. Cool thing to make. How accurate is this logarithm Bobboau made?

[At]

Heh.  The newtonian physics model depends more on FS2's physics engine than just the Inertial tensor.  The tensor itself is correct according to the mass and the ship.  To implement newtonian physics, we'd have to rip out and replace the physics engine.  I might actually try that.  I have to wonder if it'd screw with the AI, though.

We'd definitely need to change the decelerate control to "backwards acceleration".  The difference being that you could accelerate backwards.  Of course, this makes things MUCH more interesting as you can reach pretty high speeds and spiiiiiiiiiiiiiiiiiiiin....

As for hobby?  I dunno.  I did do it out of boredom.  Yep...  Might try the physics thing, too.  Sounds kinda simple... Whacks apply a torque which give it an angular acceleration over a small period of time, giving you a different angular velocity... And as well give you a different linear velocity after the impact...

Hmm, an "About face" command might be good, too, to point you in the opposite direction of your current linear velocity vector...  With the bonus of killing your angular velo vector...

And yeah, I know it's a low res integration.  Pretty much where I got the idea
Naturally, the calculator thingy would use much smaller cubes...

Logarithm?  You mean algorithm?  I'm pretty sure there's already a field of study for that moving masses stuff.  I think it's called contiuum or some such.  Not sure how reducible that would be.  And it'd have to be, since FS would be doing these calculations on the fly.

And the thing Bob-oh made was for calculating a tensor for a static shape, generally a ship.  I don't have the patience or the time to pick what he did apart, so I really can't make any good guesses about how it works.

[phreak]

Hi.  Can you code for the SCP?

[At]

Maybe in the summer.  Just so long as I don't need to make or break objects, which if I'm munging up the physics, should be just fine.  Some of the C++ object syntax scares me... >.>

Generally, if it's pretty C like, it's okay.

And yeah.  I really should be working on the school work I don't wanna do.  But... We'll see.. <.<

[StratComm]

The MOI tensor would never be calculated on the fly or even in model parse, and so would be better suited to a function either in post-conversion editing (PCS) or conversion itself (Max->POF).  Otherwise though, that's a good relatively fast approximation for a convex shape.  How it would do on non-convex models I'm somewhat uncertain of, but that shouldn't be too terribly hard to figure out.

[At]

Oh, yah.  The tensor takes way too much calculation to do on the fly.

As for non convex shapes, For the cubes approximation, it'd be easy.  You just start at one end of the bounding box and go till you encounter a polygon, then start drawing the cuboid until you hit another polygon.  And so on.  You end up with something like this.

[Bobboau]

not to disapoint you or anything, but I knew all that already, on the plus side you seem to now know about as much as I do on the subject

I could probly make a MOI calculator within the FS source, maybe I should give that a wack sometime, as it already has all the code to load up a pof...

sence the first integration wasn't *THAT* bad I think the best case would be to set up a grid along one of the planes and do simple intrsections at given gridpoints, then use the intersections to set up the start and end of a line that would be used in the integration, or just generate random rays and do the same.

[aldo_14]

not to disapoint you or anything, but I knew all that already, on the plus side you seem to now know about as much as I do on the subject

I could probly make a MOI calculator within the FS source, maybe I should give that a wack sometime, as it already has all the code to load up a pof...

Write a stub library or something; IMO it'd be far better to have a reusable conversion-time way of generating this in the tools, it makes more sense to me than at runtime.

[At]

Oh, you did?  Good.  It's still your fault, though. :P

And you writing it would prolly be better since I'm kinda in the dark as far as model stuff goes.  I was actually thinking of trying to use FS2's weapons intersection code, or some modified version, to do the rays for the approximate integration.

Hmm, think you could make something to move ships so that their CoM's are at 0? ;)

[karajorma]

Write a stub library or something; IMO it'd be far better to have a reusable conversion-time way of generating this in the tools, it makes more sense to me than at runtime.

Failing that simply have it do it only in the lab and output the information to screen so that it could be added with PCS. Not as useful as Aldo's suggestion but possibly easier to do.

[Nuke]

perhaps have a button in the lab to calculate and output the currently viewed model's moi to a logfile, that would be good. id like to get proper moi information into my models.